When you watch the stock market, you don’t just look at today’s price in isolation.
You carry a memory:

“The stock has been rising for the last few days,”
or
“The trend looks like it’s turning downward.”

You don’t memorize every single price.
You summarize the past —
and adjust your view each day as new information arrives.

This is the core intuition behind Recurrent Neural Networks (RNNs).

They are built not to process isolated facts —
but to carry memory forward,
updating it step-by-step as new inputs arrive.

Why Ordinary Neural Networks Are Not Enough

Standard feedforward neural networks behave like calculators.

You give them a set of inputs.
They process those inputs once.
They produce an output.

Each input is treated independently.
There’s no memory.
No awareness of what came before.

This is fine when everything you need is in the current input —
like predicting a house price from its area and location.

But it fails in any problem where order matters —
like stock prices, speech, or language.

The Simple Idea Behind RNNs

RNNs are networks that remember.

At every step:

• They take the current input ($x_t$),
• Combine it with what they already know (previous memory $h_{t-1}$),
• Update their hidden state (new memory $h_t$).

Each step is not a fresh calculation.
It is an update to the ongoing story.

Mathematically, the idea is simple:

\[h_t = \text{function of}(h_{t-1}, x_t)\]

or even more intuitively:

\[\text{New Memory} = \text{Mix of (Old Memory + New Input)}\]

That’s it.

A Small Intuition: What the Hidden State Really Is

You can think of the hidden state as a compressed memory.

At each step, the RNN does not store everything that happened in the past.
Instead, it stores a small summary —
just enough to make good predictions about what comes next.

This summary — the hidden state — could capture things like:

• The general trend of stock prices (rising, falling, volatile),
• The topic of a conversation (talking about food, travel, work),
• The phase of a machine operation (startup, steady running, shutdown).

In simple cases, the hidden state might just be a few numbers.
For example, if the hidden state dimension is 10,
then at every step, the RNN carries a 10-dimensional vector:

\[h_t = \begin{bmatrix} 0.8 \\ -0.2 \\ 0.1 \\ \vdots \\ 0.3 \end{bmatrix}\]

These numbers encode the important aspects of the past —
compressed, summarized, and ready to be updated by new input.

Thus:

• The hidden state is not raw memory (not a tape recorder),
• It is a refined, useful summary the network builds and evolves.

Each new input slightly nudges the hidden state —
adjusting what the network believes about the ongoing story.

A Tiny Example: Tracking Stock Trends

Imagine tracking daily stock movements:

• Day 1: $+2$ (price rises a lot)
• Day 2: $-1$ (small dip)
• Day 3: $+1.5$ (rises again)

You don’t restart your memory each day.
You carry forward a belief about the overall trend —
adjusting it each day.

An RNN does the same:

• After $+2$: Memory becomes strongly positive (market rising).
• After $-1$: Memory weakens slightly (small dip).
• After $+1.5$: Memory strengthens upward again (reaffirming rise).

Each day’s memory depends on:

• Yesterday’s belief (hidden state $h_{t-1}$),
• Today’s change (input $x_t$).

Thus, memory evolves — it does not reset.

Why This Matters

Because the real world happens step-by-step.

• Stock prices change daily.
• Words in a sentence arrive one after another.
• A robot’s sensor readings update continuously.

If a model forgets after every input, it cannot understand patterns that unfold over time.

RNNs bring continuity into machine learning —
carrying memory forward, adapting as new inputs arrive.

The Big Shift

Feedforward networks map:

\[\text{Input} \quad \to \quad \text{Output}\]

One-shot.

RNNs map:

\[(x_1, x_2, x_3, \dots) \quad \to \quad (y_1, y_2, y_3, \dots)\]

but carry hidden state forward internally:

\[h_0 \to h_1 \to h_2 \to h_3 \to \dots\]

Each new output is shaped not just by the current input —
but by everything remembered so far.

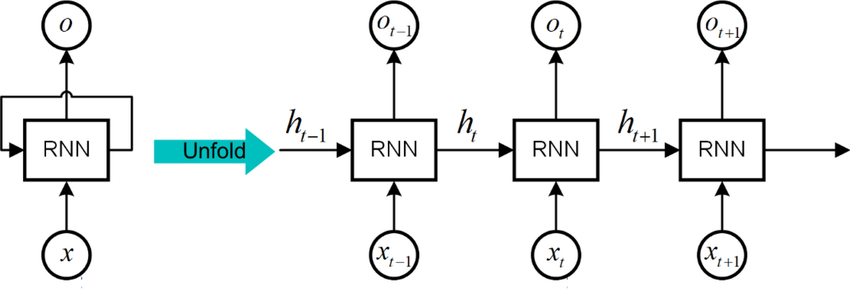Source: Adapted from Shaofeng He et al., 2023.

Plain Words Summary:

Symbol	Meaning
$x_t$	Input at time $t$ (e.g., today’s stock price change, today’s word)
$h_t$	Hidden state at time $t$ (summarized memory)
$O_t$	Output at time $t$ (what we predict or generate based on memory so far)

✅ So in your schematic:

• Horizontal arrows = hidden state memory $h_t$ flowing through time.
• Vertical upward arrows = outputs $o_t$ produced at each step (based on the current memory).

✅ $O_t$ is the actual prediction at each time step.

Conclusion

Recurrent Neural Networks are built on a simple human insight:

The past matters.
New information adjusts, but does not erase, what we already know.

Every step is a conversation between memory and new experience.

That small idea —
to carry memory forward and update it carefully —
is what powers sequence models across language, finance, control systems, and beyond.

Understanding RNNs is not about memorizing formulas. It’s about realizing that learning through time is different from learning in isolation — and that memory is the bridge between yesterday and today.

---

Note:
This post was developed with structured human domain expertise, supported by AI for clarity and organization.
Despite careful construction, subtle errors or gaps may exist. If you spot anything unclear or have suggestions, please reach out via our members-only chat — your feedback helps us make this resource even better for everyone!